线性表的抽象数据类型定义
ADT 线性表(List)
Data
线性表的数据对象集合为{a1,a2,…,ai,ai+1,…,an-1,an},每个元素的类型为DataType。其中,除第一个元素a1外,每个元素都有一个直接前驱元素,除最后一个元素an外,每个元素都有一个直接后继元素,数据元素之间的关系是一对一的
Operation:
initList(List *list): 初始化操作,建立一个空的线性表list
listEmpty(List list):若线性表为空,则返回true,否则返回false
clearList(List *list):将线性表清空
getElement(List list,int i,ElementType *e):获取线性表第i个元素的值,该值赋值给e
locateElement(List list,ElementType e):在线性表中查找与给定e值相等的元素,如果查找成功则返回元素在线性表中的序号,否则返回0
listInsert(List *list,int i,ElementType e):在线性表序号为i处,新建并插入值为e的新元素,插入成功返回TRUE,否则返回FALSE
listDelete(List list,int i,ElementType e):删除线性表中序号为i的元素,并用e来存储元素值返回给调用方,如果删除成功返回TRUE,否则返回FALSE
注:这个定义对于线性表的顺序存储与链式存储都是适用的
线性表顺序存储定义
线性表的顺序存储结构,指的是用一段地址连续的存储单元依次存储线性表的数据元素。
若存在线性表{a1,a2,…,ai,ai+1,…,an-1,an},LOC表示求地址操作,每个数据元素需要m存储空间,则有LOC(ai+1)=LOC(ai)+m, LOC(ai)=LOC(a1)+(i-1)*m
线性表顺序存储结构
1 |
|
这里,我们就发现线性表顺序存储结构的三个特点
- 线性表的最大存储容量:数组长度MAXSIZE
- length当前存储的数据元素的个数,即当前线性表的长度
- 存储空间的起始位置:数组data,它的存储位置就是存储空间的存储位置
线性表顺序存储结构的插入、删除操作
插入操作算法描述
- 检查当前线性表的长度是否等于线性表的最大存储容量,若是则返回FAILURE,然后检查插入位置是否在1至线性表长度+1,若不是则返回FAILURE
- 若i <= 线性表长度,意味着需要移动元素,从线性表最后那个元素开始,到第i个元素,每个元素往后移动一个位置
- 将要插入的元素填入位置e
- 线性表的长度+1
注意:这里第i个元素,在C语言数组的序号表示为i-1
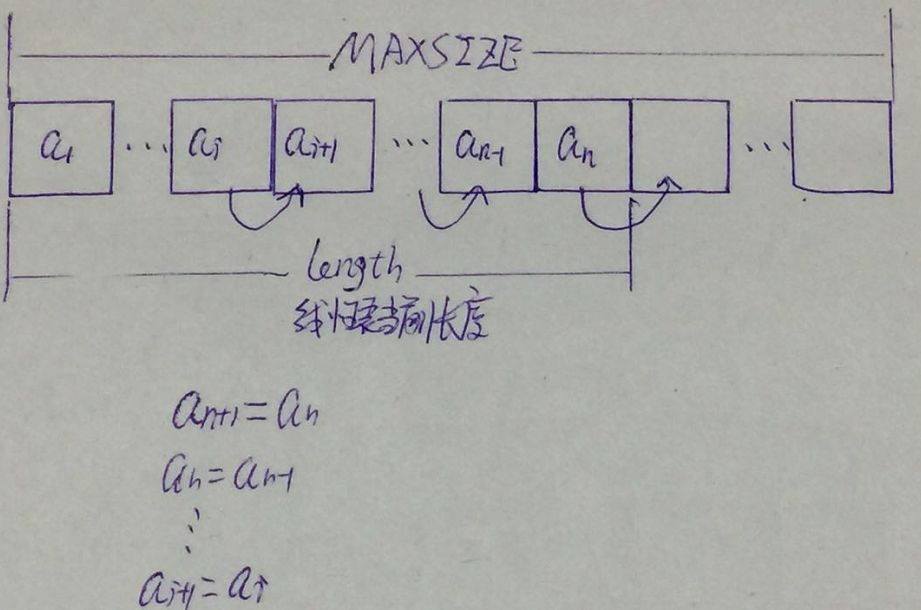
1 | Status listInsert(SqList *sqList, int i, ElementType e) { |
插入操作时间复杂度为O(n)
删除操作算法描述
- 如果删除元素位置不合理,则返回FAILURE
- 用e存储要被删除的元素
- 如果删除的元素位置不在表尾,则需要移动元素,从第i+1元素开始至第length个元素,每个元素向前移动一个位置
- 线性表长度-1
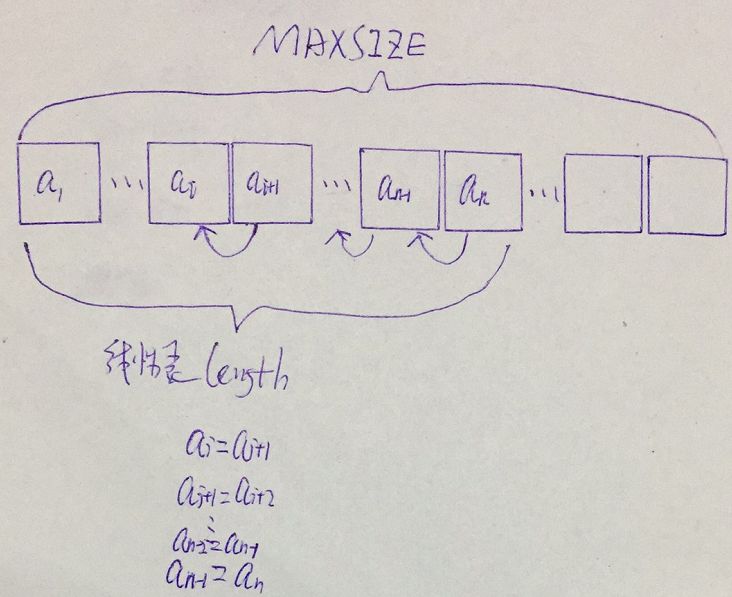
1 | Status listDelete(SqList *sqList, int i, ElementType *e) { |
删除操作时间复杂度为O(n)
线性表顺序存储实现的完整代码
1 |
|
线性表顺序存储的优缺点
优点
- 无需为表示表中的元素之间的逻辑关系,而额外增加存储空间
- 可以快速存取表中任一位置的元素,存取元素时间复杂度为O(1)
缺点
- 插入、删除元素时,需要移动大量元素
- 当线性表长度变化比较大的时候,难以估计线性表的存储容量
- 容易造成存储空间的“碎片”
